巧用“转化法”求面积(3)
"转化法"求面积(3)。 家人们,这是一道小升初的几何图形问题。知道有一个直角三角形,a、b、c里边有一个正方形,知道了a、d和c、d的长,求图中两个阴影部分的和。 当拿到这道题的时候,看到这两个小三角形当中都只给了斜边,能用三角形的面积公式分别求出两个面积,然后再相加吗?方法肯定是行不通的,应该怎么办?所以要用到一个重要的方法:转化。把这两个小三角形转化成一个和它们面积相等的大三角形,那个三角形的面积非常好求,就能解决这个问题。 怎么转化? ·首先把三角形ade切下来,补到这。同学们心里一定会有疑惑,说老师补到这以后能保证一定就是这样的吗? ·首先正方形保证了ed和fd相等,所以能保证这个点落在这。 ·由于这里的角是直角,挪下来以后到这仍然是直角,保证了bfc三点贡献。 ·又因为这里是九十度,所以角一加上角二就等于九十度。把这个角一挪到这来以后,角一和角二的和仍然是一个九十度,就保证了三角形dch仍然为一个直角三角形。这样dh的长就等于四厘米,就能求出阴影部分的面积,等于两条直角边乘积的一半。 同学们,转化的思想是一种重要的数学思想,通过做题能够培养孩子的转化能力和良好的思维习惯,提升他们的数学素养。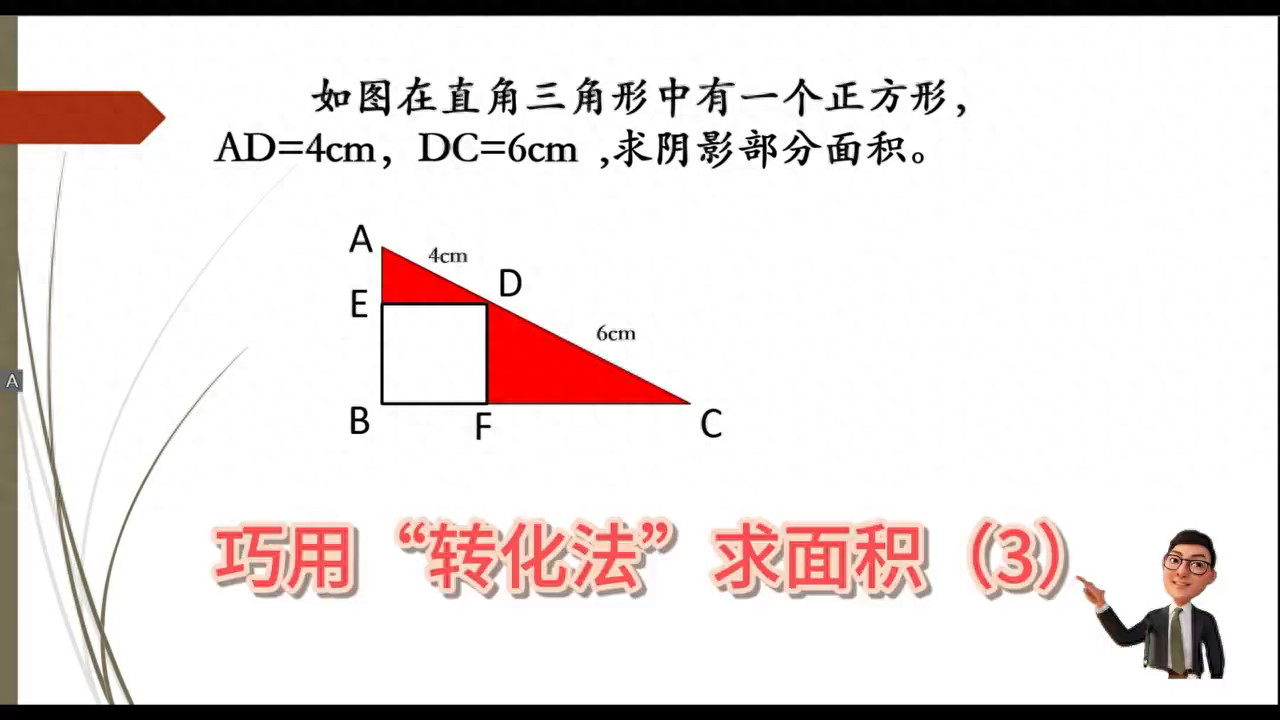
- 最近发表
- 随机阅读
-
- 中国美术史大家王伯敏三十三幅经典山水绘画作品赏析
- 事关职称申报,这些你需要知道
- “谁开的这辆车?他救了我妈的命!”
- 天蝎座财从四面八方涌来,今年你将收钱收到手软,接财运
- 新华全媒+丨这些面食为何火遍全国?——来自2022中国非遗面食大会的观察
- 兰花是不是春天开花吗?
- 如何申请职业教育资格证
- 这些铁路工种,你真的知道吗?
- 社保卡紧急提醒!速看!
- 劳务派遣的真实感受,什么是派遣?正式员工与派遣有何区别
- 厉害了,我的豪大大
- 谷寿夫枪决过程:到刑场后手脚瘫软,被市民打掉帽子:你也有今天
- 秒收:3DGIS中几种常见的透明表达方式
- 省安委办、消安办联合行动!剑指三类重点场所!
- 难忘的出差经历之一
- 海尔官博招实习生 争着拿快递也成应聘条件
- 华为回应AITO问界成立销服联合工作组:跟话语权无关
- 30项文化活动等您来!北京市属公园五一假期这样玩→
- 国学经典:《声律启蒙》原文及注解
- 高中生物老师是个女的,讲到生理部分时,她向一男生提问:)
- 猜你喜欢
-
- 搜索
-
- 友情链接
-