巧用“割补法”求面积#趣味数学
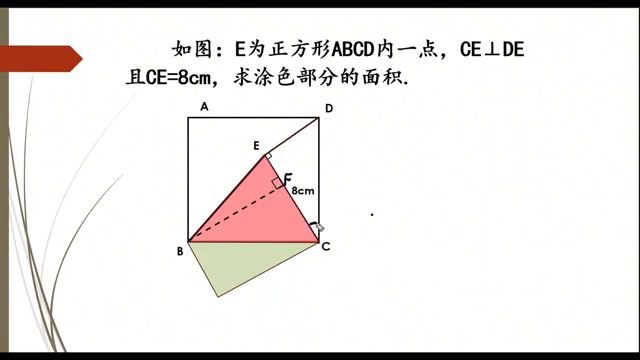
巧用"割补法"求面积(1)。 家人们,如果我说这道题难住了百分之九十的小学生,你想来挑战一下吗?知道正方形内有一个点E,CE和DE是垂直的,知道CE的长等于八厘米,求涂色部分的面积。 当我读完题,一定有人会想说:老师,这么简单的问题让你说的神乎其神,不就是正全等吗?从B点向底边做垂线,得到一个三角形BCF。假设用F来表示,证明三角形BCF和三角形CDE全等,就能证出BF等于CE等于八厘米。再用底乘高除以二,得到三角形的面积。 这种方法当然非常好,但是小学生并没有学过全等,就要想一种小学生能够接受的办法:割补法。把三角形EDC割下来,补到正方形的下边,就会发现这两个角原来相加是等于九十度的。把角一拿到下边,它俩的和仍然是九十度,这里是九十度,这里又是九十度。 一个四边形如果它的三个角都是九十度,一定就是长方形。就知道长方形的对边是相等的,从而求出了涂色部分的高也为八厘米。用底乘高除以二,就求出了它的面积为三十二平方厘米。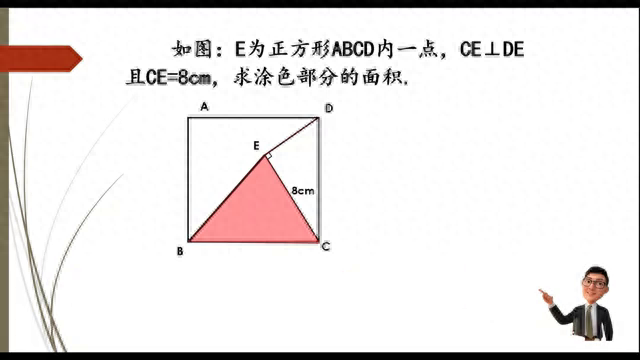
-
上一篇
-
下一篇
- 最近发表
- 随机阅读
-
- 荆州市城管执法委运用“黑科技” 投入新型打捞船 “智”理护城河水体
- 浙江参保人看过来!2024社保基数、养老金、医保缴费都有新变化!
- 5800+!燕郊烧鸽子高端餐饮招聘啦
- 西安这几家花甲粉集齐了鲜香麻辣,分分钟召唤起食欲
- 想闯进世赛有多难?万里挑一!第47届世界技能大赛集中考核结束
- 5月22日开始申领!丰泽这8类人可享社保补贴
- 一辆车是如何被造出来的!
- 深度揭秘《国学国画书法培训加盟》里的重重黑幕
- 精准推进参保扩面,日照市人社局发布社会保险经办工作有关情况
- 靠“自来水”的视障服务app:有人一年求助300多次,志愿者抢单免费服务
- 如何判断“假外包,真派遣”?外包与派遣的本质区别是什么?
- 美国隐蔽行动的掩护组织
- 被拖欠工资怎么办?别着急,教你几招
- 请查收!洛阳市社保业务经办服务电话
- 江西省本级养老保险待遇资格认证公布八类方式
- 8项社保业务可在“亲清在线”秒审秒办!
- 欧阳淞:构筑起以建党精神为核心的中国共产党人的精神谱系
- 身份证上的“X”读什么?如何买火车票?
- 内蒙古监狱管理局第一医院:推行“7S”管理规范基础工作
- “太和顾问”增效人力成本 助力企业发展
- 猜你喜欢
-
- 搜索
-
- 友情链接
-